Panjang Busur Dan Luas Juring Lingkaran

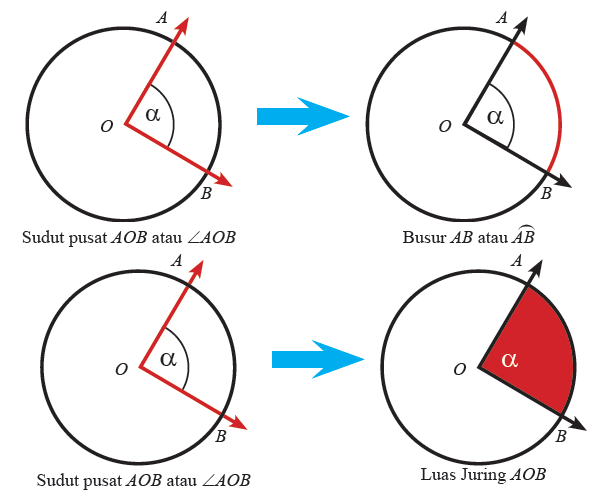
Sebuah bulat mempunyai beberapa unsur yang membentuk bulat tersebut. Unsur-unsur bulat antara lain : Busur, Jari-jari, Diameter, Tali busur, Apotema, Juring, dan tembereng. Busur ialah himpunan titik-titik yang berupa kurva lengkung (baik terbuka atau tertutup) dan berhimpit dengan lingkaran. Sedangkan Juring bulat ialah kawasan di dalam bulat yang dibatasi oleh busur dan dua jari-jari. Panjang busur sebanding dengan sudut sentra yang menghadapnya. Begitupun luas juring sebanding dengan sudut sentra yang bersesuaian dengan juring tersebut. Perhatikan gambar berikut.

Dari gambar di atas kita sanggup amati panjang busur AB bersesuaian dengan sudut sentra α, begitupun luas juring AOB bersesuaian dengan sudut sentra α.Ukuran sudut sentra bulat ialah antara 0° hingga 360°.

Rumus keliling dan luas bulat yang sudah diperoleh dikala SD yaitu Rumus keliling bulat yaitu 2πr atau πd, Rumus luas bulat yaitu πr² atau 1/4 πd². Dimana r ialah jari-jari lingkaran, d ialah diameter lingkaran, dan π ialah suatu konstanta yang nilainya 3,14 atau 22/7.

Nilai konstanta π yang kini kita kenal ialah rasio antara keliling bulat dengan diameternya. Jika dinyatakan dengan simbol K/d = π. Dengan kata lain π x d. Karena d=2r, maka  hubungan tersebut sanggup juga dinyatakan K = 2πr.

Ukuran sudut sentra satu bulat penuh ialah antara 0° hingga 360°. Luas juring dan panjang busur sebanding dengan besarnya sudut pusat. Artinya semakin besar sudut pusat, semakin besar pula luas juring dan panjang busurnya.

Ayo Kita Amati
Amati garis yang berwarna merah ialah gambar panjang busur bulat yang bersesuaian dengan
sudut pusatnya masing-masing.

Rasio sudut sentra α terhadap 360°	Rasio panjang busur terhadap keliling lingkaran	Rasio luas juring terhadap luas lingkaran
α/360°	Panjang busur/K	Luas Juring/Luas Lingkaran
270 360°	270 = 3 360° 4	270° = 270 = 3 360° 4
180 360°	180 = 1 360° 2	180° = 180 = 1 360° 2
120 360°	90 = 1 360° 3	120° = 120 = 1 360° 3
90 360°	60 = 1 360° 4	90° = 90 = 1 360° 4
60 360°	30 = 1 360° 6	60°= 60 = 1 360° 6
α 360°	α = Panjang Bususr 360° Keliling	α= α = Luas Juring 360° L Lingkaran

Latihan
1. Tentukan luas juring bulat yang diketahui sudut pusatnya 70°dan jari-jarinya 10 cm

Luas Juring =	α	x πr²
	360°

Luas Juring =	70	x 3.14 x 10 x 10
	360°

= 61,055

2. Tentukan panjang busur bulat yang diketahui sudut pusatnya 35°dan jari-jarinya 7 cm .

Panjang Busur =	α	x 2πr
	360°

Luas Juring =	5	x 2 x 3,14 x 7
	360°

= 4,28

3. Lingkaran A mempunyai jari-jari 14 cm. Tentukan sudut sentra dan jari-jari suatu juring lingkaran
lain biar mempunyai luas yang sama dengan bulat A.
Panjang busur sama dengan keliling lingkarannya dikala sudut pusatnya ialah 360°.
Luas bulat A =  πr² = 22/7. 14.14 = 616
Juring yang luanya sama dengan A ( 616) adalah
Juring yang punya sudut sentra 90 dan jari-jari 28

Luas Juring =	α	x πr²
	360°

Luas Juring =	90	x 22/7 x 28 x 28
	360°

= 616

4. Buatlah bulat A dengan jari-jari tertentu, sedemikian sehingga luasnya sama dengan juring pada bulat B dengan sudut sentra dan jari-jari tertentu. Jelaskan.
Misalkan:
Lingkaran A mempunyai jari-jari 7 cm
Lingkaran B mempunyai jari-jari 14 cm

Dengan perhitungan, Luas bulat A:
= π r² = 22/7 x 7² = 154 cm²

Dan luas bulat B:
= πr² = 22/7 x 14² = 22 x 2 x 14 = 616 cm²

Dengan demikian:
Sudut sentra untuk juring pada bulat B adalah:
a/360 = La/Lb
a/360 = 154/616
a/360 = 1/4
a = 360/4
a = 90°

Dari perhitungan tersebut sanggup disimpulkan Luas juring B lebih dari Luas juring A

5. Diketahui:
(1) Lingkaran penuh dengan jari-jari r,
(2) setengah bulat dengan jari-jari 2r.
Tentukan manakah yang kelilingnya lebih besar?
1.) K = 2πr
2.) 1/2 K = 1/2 x 2πr = πr + 2r

Misal r = 7, maka
1) K = 2πr
= 2 X 22/7 X 7
= 44

2.) K = πr + 2r
= 22/7 X 7 + 2X7
= 22 + 14
= 36
Jadi, keliling yang lebih besar ialah yang no. 1)